Saber Jafarpour

Research Assistant Professor
Department of Electrical, Computer, and Energy Engineering
University of Colorado Boulder
Email: saber.jafarpour@colorado.edu

Home Research Publications Teaching Talks C.V. Google Scholar



My research is in the broad area of control theory and autonomy with focue on developing provable guarantees for safety, learning, and control of robotics and cyber-physcial systems. Recent technological advances are changing the way autonomous systems are being operated and are opening up new possibilities for their control and coordination. Despite the benefits of these emerging technologies, safety and reliability consideration pose substantial challenges in fully utilizing them in real-world applications. I leverage tools and concepts from systems and control theory for performance analysis of optimization and machine learning algorithms and for safety assurance of modern autonomous systems. 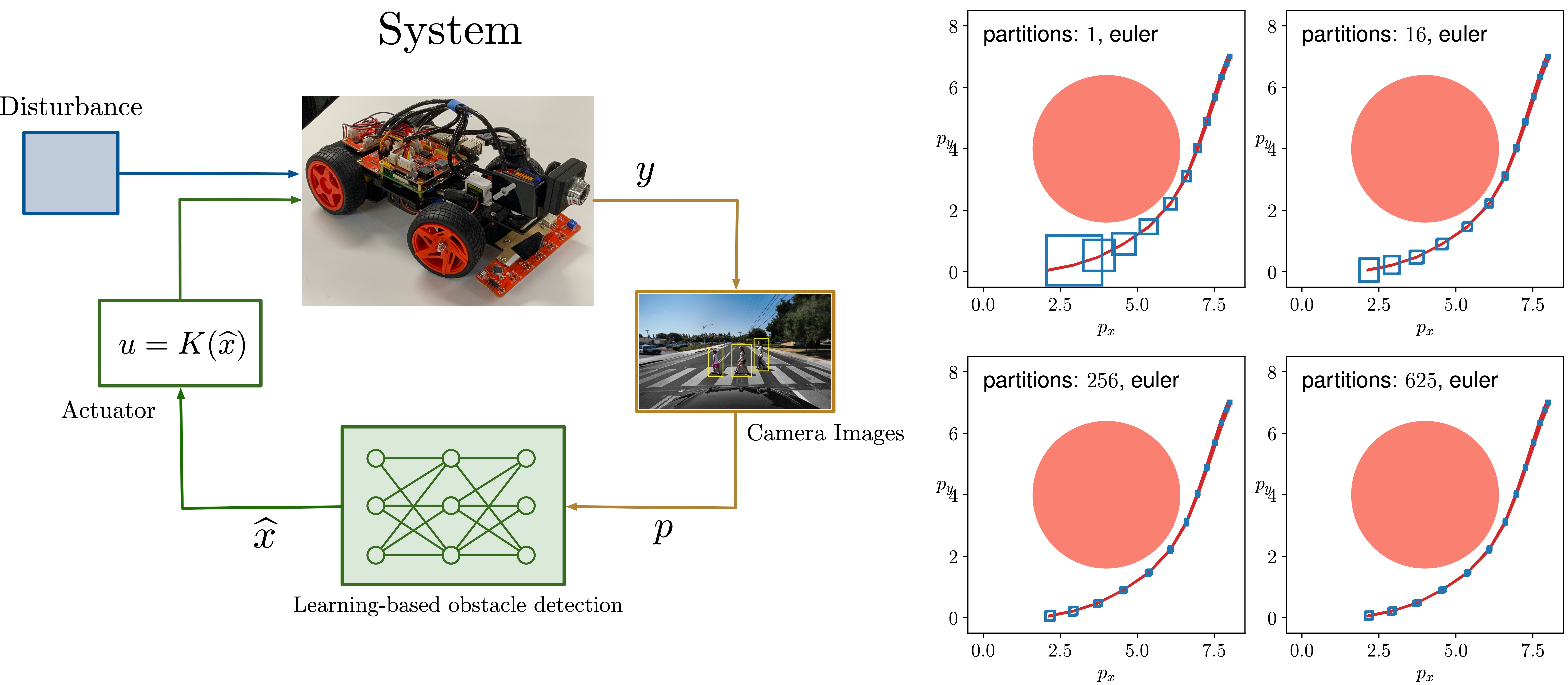My photo



Safety Assurance for Learning-enabled Systems

Machine learning components are increasingly being deployed in safety-critical autonomous systems, driven by the availability of abundant data and their computational efficiency. However, these learning-based components often lack formal performance guarantees. Moreover, due to their high-dimensional and nonlinear nature, traditional verification methods struggle to scale effectively for ensuring their safety. My research focuses on the safety of such autonomous systems from a reachability perspective. By leveraging state-of-the-art verification techniques for learning algorithms, we develop computationally efficient tools to estimate the reachable sets of learning-enabled systems. 		My photo

Selected Publications:



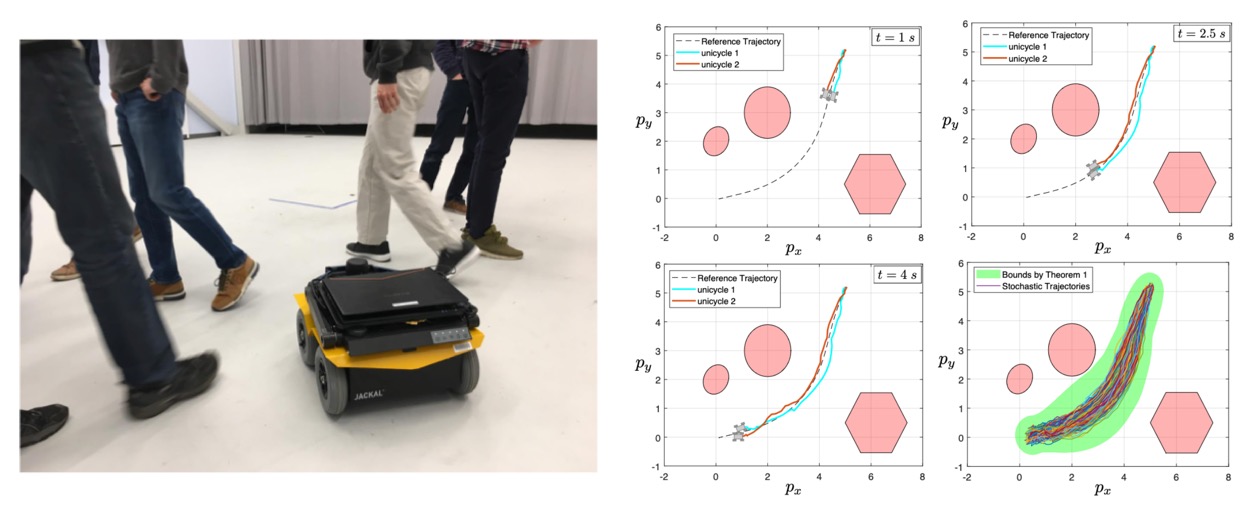
Verification and Control of Stochastic Systems

Many real-world systems operate under uncertainties that are unbounded, unpredictable, and highly variable over time. For such uncertainties, providing tight bounds is impractical, making it more appropriate to model them as stochastic variables and apply probabilistic methods for analysis. However, for general nonlinear systems, the existing results in the literature fail to accurately capture the impact of stochastic noise on system dynamics. We develop a comprehensive theoretical and algorithmic framework that separates the effect of between worst-case and stochastic uncertainties, offering statistically tight estimates of the reachable sets of stochastic systems. A key advantage of our framework is its adaptability to any verification and synthesis algorithm for deterministic systems. 		My photo

Selected Publications:


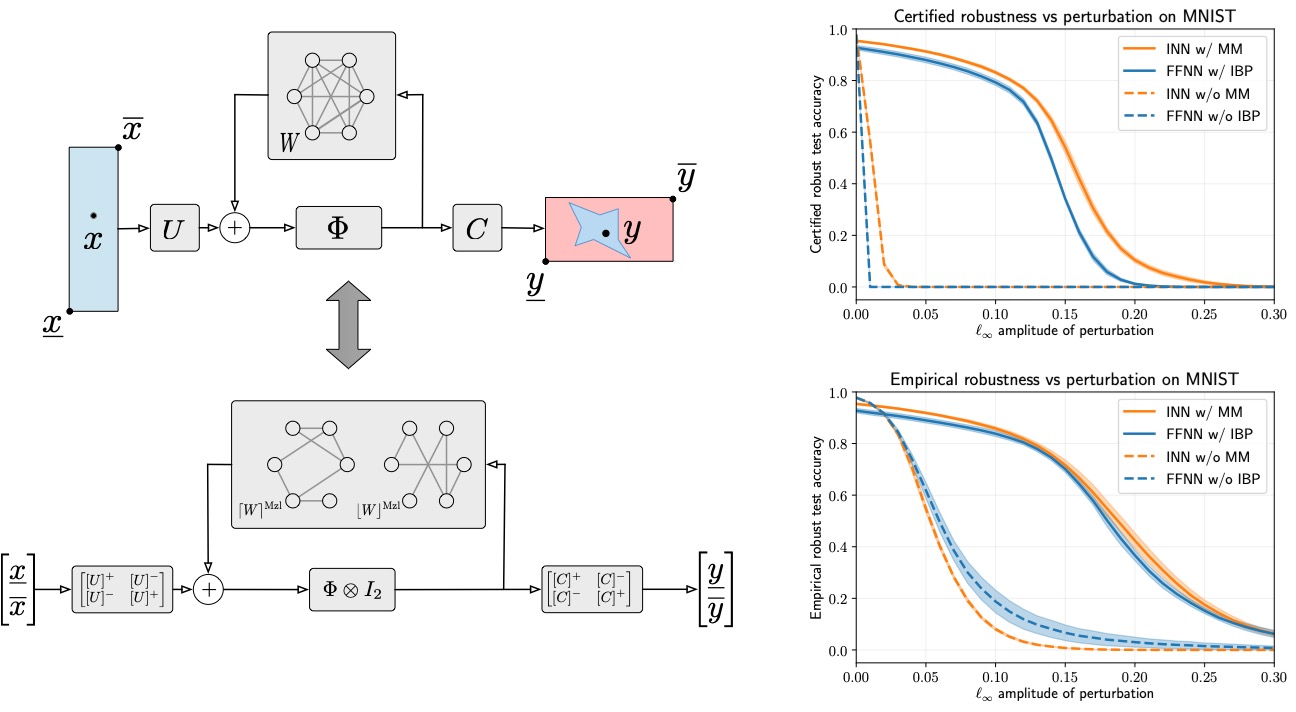
Guarantees for Algorithms via Contraction Theory

Many autonomous systems seamlessly integrate dynamical models with optimization and learning algorithms. These systems can exhibit a wide range of asymptotic and transient behaviors, from convergence to reference trajectories to periodic orbits. To ensure their reliable performance, it is crucial to provide provable guarantees for their behavior. Contraction theory, a classical framework for studying dynamical systems, that provide guarantees for systems based upon the incrementally distance between trajectories. However, the analysis and design of optimization and learning algorithms extend beyond the scope of classical contraction theory. We develop extensions of classical contraction theory to investigate the stability and robustness properties of autonomous systems that incorporate optimization and learning algorithms. 		My photo

Selected Publications:


Resilience of Large-scale Autonomous Systems

Large-scale autonomous systems, such as multi-agent robotic systems and infrastructure networks, are becoming ubiquitous in modern society. With the increasing integration of intelligent sensing and actuation devices, these systems are becoming more vulnerable to disturbances. Ensuring robustness of these complex systems against disruptions and adversarial events is a critical task for system operators. Ensuring the robustness of these complex systems against disruptions and adversarial events is a critical task for operators. A key challenge in guaranteeing their robustness is the sheer size of these networks. We analyze these large-scale autonomous systems from a network perspective and develop computationally efficient methods to certify their safety and stability. 		My photo

Selected Publications:


Past Research Activities:

During my PhD, I participated in the following seminars held at Queen's University.